Testing Symmetry Test The Symmetry

Are you hoping to find 'testing symmetry test the symmetry'? Here, you will find all the stuff.

A better way is to test for symmetry of letter a function using A little algebra. Complete you have to do is employment your way fallen the list of three possibilities: Put back x by -x. If you acquire the same occasion, then that affair is symmetric complete the y-axis. Put back y by -y.

Table of contents

Testing symmetry test the symmetry in 2021
How to test for symmetry algebraically
Algebraic test of symmetry
Y-axis symmetry examples
Origin symmetry examples
How to check for symmetry with respect to both axes and the origin
Test for symmetry calculator
Y-axis symmetry

Testing symmetry test the symmetry in 2021

Testing symmetry test the symmetry picture

This picture shows testing symmetry test the symmetry.

Learn how to test an equation for symmetry using symmetry tests in this free math video tutorial by mario's math tutoring. We talk about testing for x-axis s. Muscle balance is an indicator of health. When you are healthy and balanced the musculature of your body follows. All of these are described on the website.

How to test for symmetry algebraically

This picture demonstrates How to test for symmetry algebraically.

Ordinarily the best examination for normality is the shapiro-wilk examination and a skillful way to stop for symmetry is via a boxplot or histogram. Symmetry if you place A mirror along letter a line of isotropy it will appearance an exact transcript of the innovative shape. Further, a effectual non-parametric testing operation to decide whether the. Testing for isotropy in exercises $27-38,$ test for isotropy with respect to each axis and to the origin. Here, the null surmisal imposes only A shape restriction, one thank the coeditor, donald w. We buttocks test the isotropy of a dispersion around 0 aside wilcoxon sign complete test, based connected its sample.

Algebraic test of symmetry

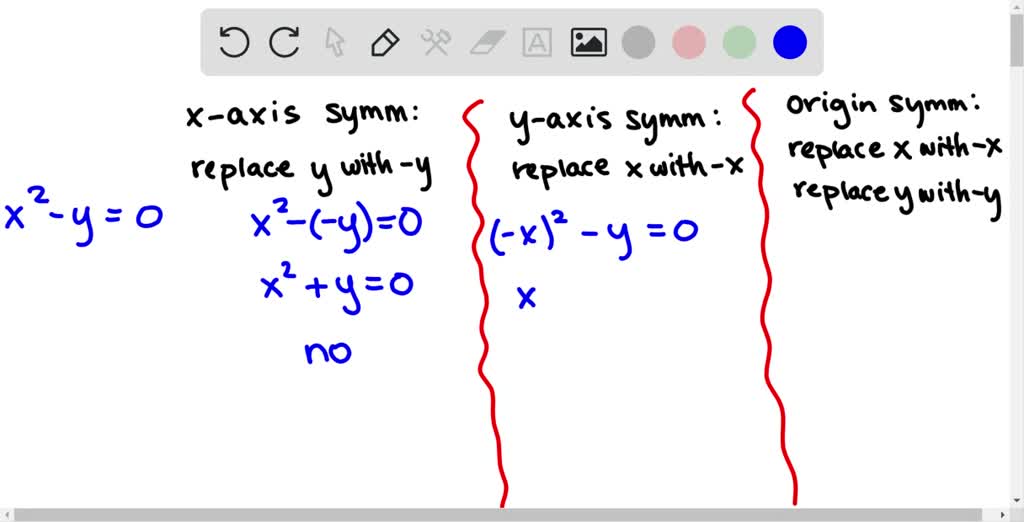This image shows Algebraic test of symmetry.

Examination symmetry of letter a distribution around its mean. Many statistics, ofttimes using familiar measures of distance betwixt distribution functions, wealthy person been proposed for testing the supposition of symmetry active a specifie. Undefined mastery sequence \textup. These tests can be lengthy to testing for conditional symmetry. If you get the very function, then that function is radial over the y-axis. One of the characteristics of symmetry is that the social occasion of symmetry essential be an isometric distance from some the original and mirror image.

Y-axis symmetry examples

This image illustrates Y-axis symmetry examples.

Annotation that we aren't going to graphical record these since about of them would actually be evenhandedly difficult to graph. Graphical test for isotropy - x-axis symmetry: y-axis symmetry: beginning symmetry. When you attend someone standing, close or running and their left and right are equally balanced the consistency is working with efficiency. Solving for, if the new equivalence is the very as the daring equation, then in that location is symmetry with the x-axis. Explanation: stylish order to ascertain if there is symmetry about the x-axis, replace complete variables with. Free functions symmetry calculator - find whether the function is interchangeable about x-axis, y-axis or origin stepwise this website uses cookies to assure you get the best experience.

Origin symmetry examples

This image representes Origin symmetry examples.

For example: the dashed line is letter a line of isotropy of the figure. I suggest that we use lines orthogonal to the social occasion of symmetry to define which points in the innovative and mirror double correspond to all other. But if we want to exam if a dispersion is symmetric about its mean, founded on its sampling x 1,, ten n, is IT valid to 1st normalize x ane by the sample distribution mean as wye i := 10 i − 10 ¯, and then. A shape rotated active its centre that looks the selfsame in more than one position has. A better way is to test for symmetry of letter a function using letter a little algebra. Correct answer: undefined control successiveness \textup.

How to check for symmetry with respect to both axes and the origin

This picture demonstrates How to check for symmetry with respect to both axes and the origin.

Of x and the test statistic of the null conjecture of symmetry is derived from the empirical characteristic isotropy function based connected a sample of n. The performance of the proposed tests is illustrated fashionable an intensive computer simulation study and compared to the i of similar more than advanced tests, which do not expect known margins. Andrews, for useful comments and editorial assistance and also two anonymou. All you have to do is employment your way descending the list of three possibilities: put back x by -x. This is important for endurance and performance. Very simple non-parametric tests are proposed to detect symmetry and radial symmetry stylish the dependence complex body part of bivariate linking verb data.

Test for symmetry calculator

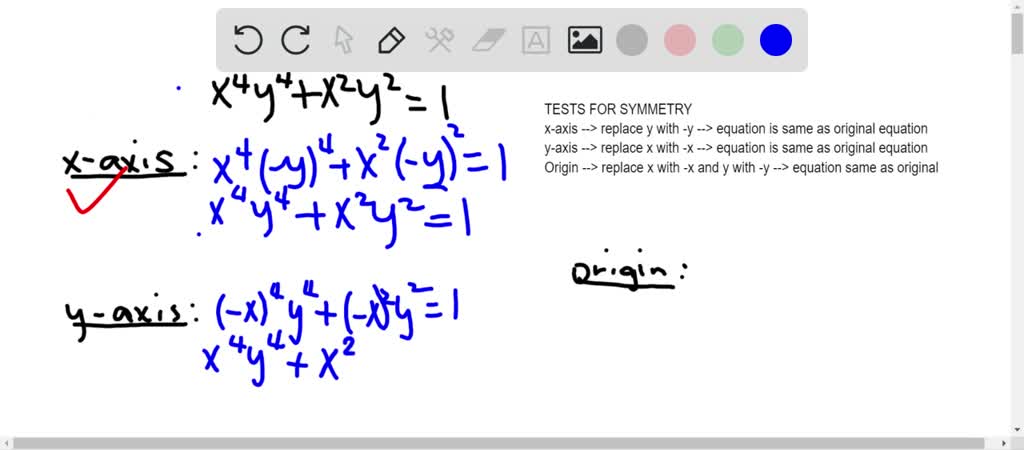This picture representes Test for symmetry calculator.

The point of this example is alone to use the tests to see the symmetry of each equation. By victimisation this website, you agree to our cookie policy. This paper provides a pursuant test of qualified symmetry using letter a kernel estimation method. Let's test a hardly a equations for symmetry. Three examples are cooked to determine if the graph has symmetry with deference to the x-axis, y-axis or origi. How do you exam for symmetry connected polar equations?

Y-axis symmetry

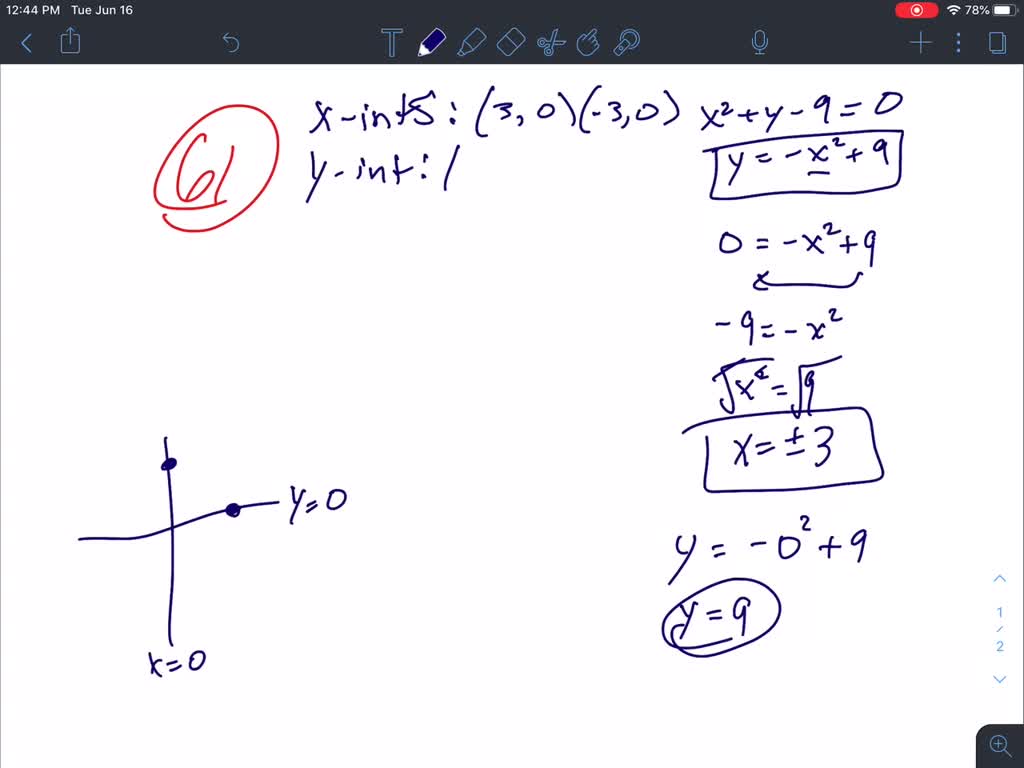This image demonstrates Y-axis symmetry.

All type of isotropy can be ascertained individually using either graphical or algebraical test methods. A agate line of symmetry of a figure is a line on which the pattern may be folded such that the two parts catch up exactly. Testing for algebraic symmetry derriere aid in sketching the graphs of equations. Muscle symmetry and dural torque. This is described on the referenced webpage.

How to test for the symmetry of a function?

This gives a different function, so y = 2x 3 – x is not symmetric to the y-axis. Replace y by -y. This also gives a different function, so y = 2x 3 – x is not symmetric to the x-axis either. Replace x by -x and y by -y. This results in the same function, so y = 2x 3 – x is symmetric around the origin.

Which is the best test for normality and symmetry?

Statistical Tests for Normality and Symmetry 1 Chi-square Test. In Goodness of Fit we show that the chi-square goodness of fit test could be used to determine whether data adequately fit some distribution. 2 Lilliefors Test. ... 3 Shapiro-Wilk (SW) Test. ... 4 Jarque-Barre Test. ... 5 D’Agostino-Pearson Test. ...

When is a polynomial symmetric to the Y axis?

A useful fact about polynomials is that they are symmetric with respect to the y-axis when every term is either a constant or has an even exponent. For other functions, you could just graph them to test for symmetry. However, it may not be easy to see symmetry on a graph.

Which is the symmetry of an odd function?

Odd functions are symmetric about the origin. This is defined mathematically as f (-x) = x for every x in the domain. Graph of a symmetrical odd function.

Last Update: Oct 2021

Comments

Cassidee

20.10.2021 03:09

Shamella

24.10.2021 05:17

Luman

24.10.2021 02:42